基础排序算法

• 对一些排序算法做个归纳
• 持续更新

算法性能评估术语

• 稳定：如果a原本在b前面，而a=b时，排序之后a仍然在b的前面。

• 不稳定：如果a原本在b的前面，而a=b时，排序之后a可能出现在b的后面。

• 内排序：所有排序操作都在内存中完成。

• 外排序：通常是由于数据太大，不能同时存放在内存中，根据排序过程的需要而在外存与内存之间 数据传输才能进行。

• 时间复杂度：时间频度，一个算法执行所耗费的时间。算法中通常用数据比较次数与数据移动次数 进行衡量。

• 空间复杂度：算法执行所需要的内存大小。

• In-place：占用常数内存，不占用额外内存

• Out-place：占用额外内存

---

冒泡排序

说明

冒泡排序

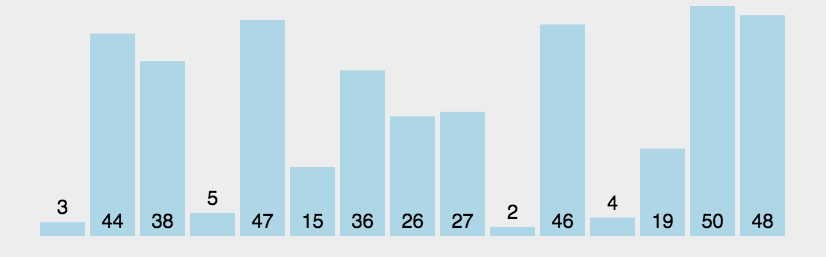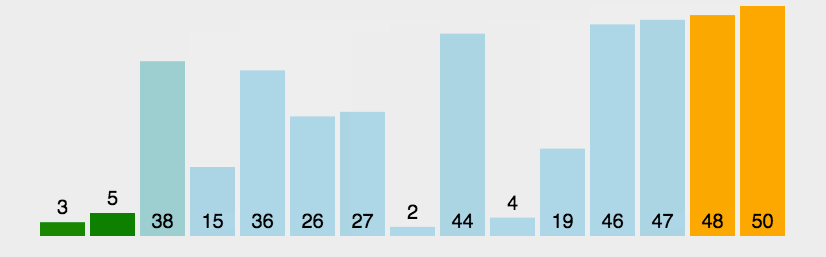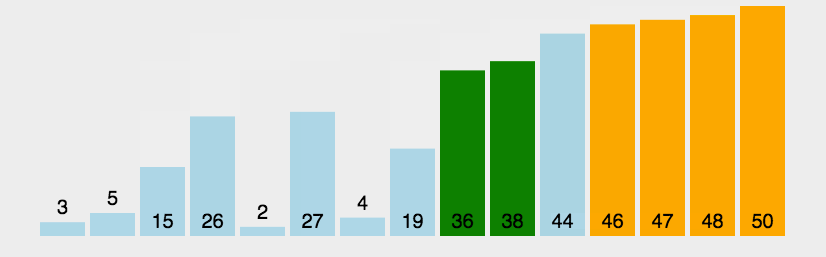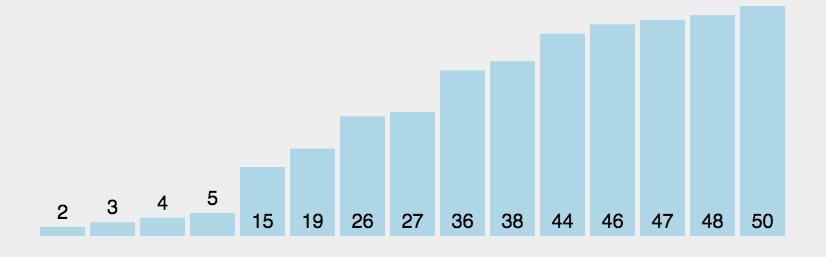
• 最基础的排序
• 算法的每⼀轮都是从左到右来⽐较元素， 进⾏单向的位置交换的

原始代码实现

void bubbleSort(int a[], int n) {		//n为元素个数
    for (int i = n - 1; i > 0; i--) {
        for (int j = 0; j < i; j++) {
            if (a[j] > a[j + 1])
                swap(a[j], a[j + 1]);
        }
    }
}

原始代码性能分析

• 最佳时间复杂度：O(N)
• 最差时间复杂度：O(N²)
• 平均时间复杂度：O(N²)
• 空间复杂度：O(1)
• 排序方式：In-place
• 稳定性：稳定

代码优化

函数模板

template<typename T,int len>
void bubbleSort(T (&arr)[len]){
    for (int i = len-1; i > 0; --i) {
        for (int j = 0; j < i; ++j) {
            if (arr[j] < arr[j+1]){
                T t = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = t;
            }
        }
    }
}

直接传入数组指针时无法用sizeof函数，故使用引用的方式

设置排序完成的标志

冒泡排序需要有两层循环，无论数组是否排好序，都会完成这两层循环，对于最差的情况，比如[9,8,7,6,5,4]，对其进行升序排序，这两层循环必不可少；但是对于[9,1,2,3,4,5]这种情况，第一遍循环结束后，整个数组就已经是升序排列的了，但是普通的冒泡排序还会继续进行循环遍历比较，这就对做了不少无用功。所以需要设置一个排序完成的标志，如果排序已经完成，就没必要再继续循环遍历了，直接跳出循环。

template<typename T,int len>
void bubbleSort(T (&arr)[len]){
    bool isSwapped;			//判段是否进行过排序，若没排序过则直接跳出循环
    for (int i = len-1; i > 0; --i) {
        isSwapped = false;
        for (int j = 0; j < i; ++j) {
            if (arr[j] > arr[j+1]){
                T t = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = t;
                isSwapped = true;
            }
        }
        if (!isSwapped)break;
    }
}

---

鸡尾酒排序

说明

鸡尾酒排序

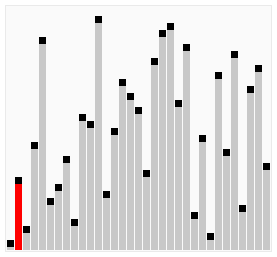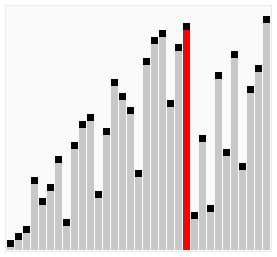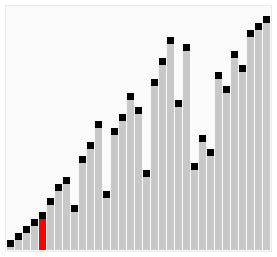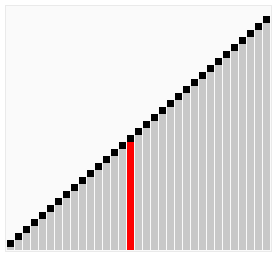
• 鸡尾酒排序是冒泡排序的优化
• 排序过程就像大摆锤一样，第一轮从左到右，第二轮从右到左，第三轮再从左到右…

原始代码实现

void Cocktail_Sort(int arr[], int sz)
{
	int tmp = 0;
	int left = 0;
	int right = sz - 1;
	for (int i = 0; i < sz / 2; i++)
	{
		//有序标记，每一轮的初始是true
		bool flag = true;

		//奇数轮，从左向右比较和交换
		for (int j = 0; j < sz - i - 1; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				tmp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = tmp;
				//有元素交换，所以不是有序，标记变为0
				flag = false;
			}
		}
		if (flag) break;

		//偶数轮之前，重新标记为1
		flag = true;

		//偶数轮，从右向左比较和交换
		for (int j = sz - i - 1; j > i; j--)
		{
			if (arr[j] < arr[j - 1])
			{
				tmp = arr[j];
				arr[j] = arr[j - 1];
				arr[j - 1] = tmp;
				//有元素交换，所以不是有序，标记变为0
				flag = false;
			}
		}
		if (flag) break;
	}
}

原始代码性能分析

鸡尾酒排序是冒泡排序的一种改进，倒并未有本质的改变，与冒泡排序的时间复杂度和空间复杂度相近，整体的性能都比较差。

• 最佳时间复杂度：O(N)
• 最差时间复杂度：O(N²)
• 平均时间复杂度：O(N²)
• 空间复杂度：O(1)
• 排序方式：In-place
• 稳定性：稳定