FOC理论准备

前言

Warn

作者本人也是在网上找资料学习的这部分内容，如有错误还请指正。本文中有对其他作者的文章的引用说明，如有忘记声明处还请大家指出。这里也非常推荐大家去看看稚晖君的教程，写得非常详尽，本文也有多处地方引用此文章的语句。

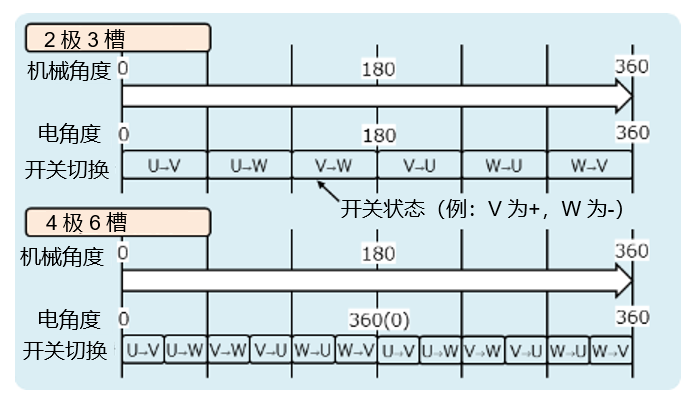
电机的机械角度和电角度

由硬件篇电机部分所描述的，极数的差异而产生了机械角度和电角度（电周期）的概念。机械角度”就是电机旋转一圈的空间几何角度。转子轴从某个位置开始旋转并返回到原位置的角度是360度。而电角度则是将对绕组（线圈）施加电压的开关的一个切换周期视为360度。

如果是2极3槽的电机，那么其机械角度和电角度是一致的。而如果是4极6槽，则其机械角度是360度，其电角度是两个周期（也可以表达为“当机械角度为180度时，电角度达到360度”，或者说“在一个电周期内转子只转半圈”）。

对于电机的编码器，其角度都是来表示转子的机械角度位置。而电机驱动器输出的电信号则是基于电角度的，因为电信号源于开关一个切换周期的反复。角度的概念已经变得非常重要，所以我们需要清楚地了解这些概念以及它们之间的关系。

无刷电机控制方式和差异

六步换相

无刷电机的六步换相（Six-Step Commutation）是一种经典的控制方式，主要用于三相无刷直流电机（BLDC）。它也被称为梯形波控制（Trapezoidal Commutation），因其电压或电流波形呈梯形得名。

六步换相的工作方式

三相BLDC电机有3根绕组（A、B、C），电机驱动器每次只通电两相，悬空一相，电流在6个步骤中按顺序换相，从而驱动电机旋转。每个电周期（Electrical Cycle）中包含6个换相步骤，每步持续60电角度，因此称为“六步”。

步骤	A相	B相	C相
1	+	-	Z
2	+	Z	-
3	Z	+	-
4	-	+	Z
5	-	Z	+
6	Z	-	+

说明：+为上桥导通，-为下桥导通，Z为高阻/不通电

• 优点：控制算法简单，成本低
• 缺点：精度差，运行不一定流畅平滑，该控制方式很难做到对电机的电流（力矩），位置做到闭环控制。采用方波控制，噪声较大。

FOC（Field-Oriented Control）控制

• 优点：转矩平稳，噪声小，响应快速。可以进行电流（力矩）、速度、位置三个闭环控制。
• 缺点：成本高，控制算法难度大

FOC控制原理

对于FOC控制过程来说，最重要的就是对电机相电流的变换和反变换。

关键前置知识

PWM, SPWM, SVPWM

PWM（Pulse Width Modulation 脉冲宽度调制）

按一定规律改变脉冲序列的脉冲宽度，以调节输出量和波形的一种调制方式。PWM是脉冲宽度调制也就是具有一定脉冲宽度的连续的方波组成。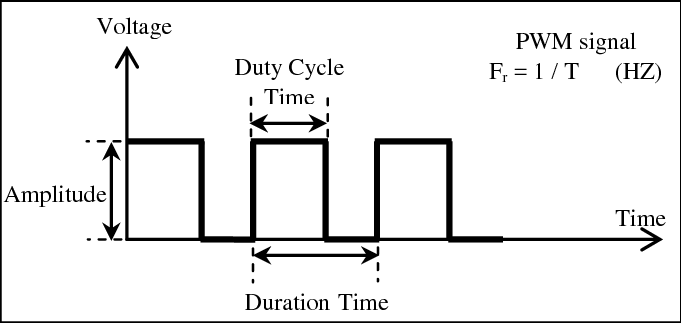

SPWM（Sinusoidal PWM 正弦脉宽调制）

该技术是基于PWM的，是对脉冲宽度进行正弦规律排列的调制方式。这样其输出可以近似为正弦波。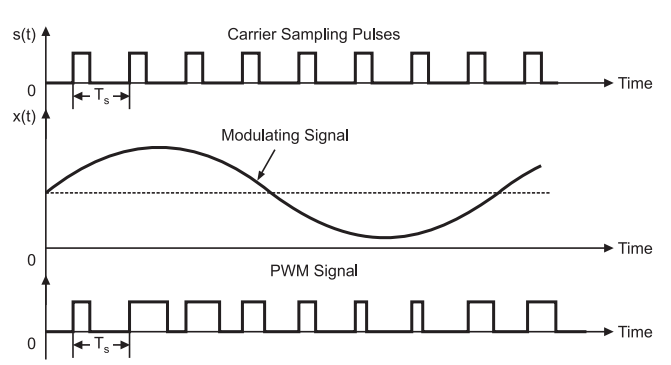

其产生的方式为正弦波和三角波相交而成，其中正弦波相当于调制波，三角波相当于载波，其生成过程如下图。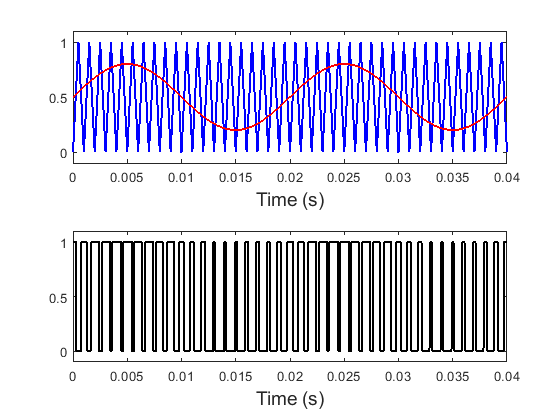

这里我们要注意，三角波（载波）的振幅要大于正弦波（调制波）的振幅，否则正弦波的波峰和波谷就会被“削去”。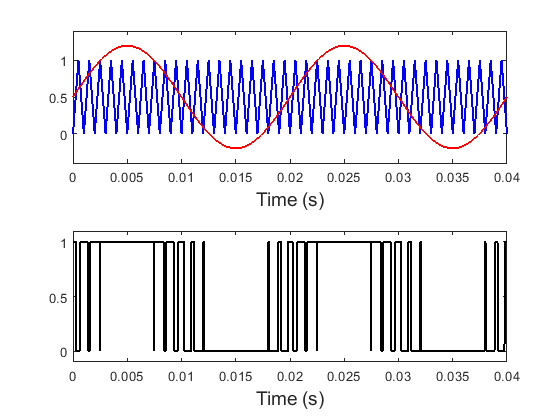

SVPWM（Space Vector Pulse Width Modulation 电压空间矢量PWM）

SVPWM和SPWM虽然名字很像，但是其时没有很大的关系。SPWM着重于生成一个可以近似于正弦波的PWM波，对于电机控制来说其关注点只在于它自己需要调制的那个正弦波。而SVPWM则是关注于电机整体，使得输出电压波形尽可能接近于理想的正弦波形，着眼于如何使电机获得理想圆形磁链轨迹！要了解SVPWM就得先了解什么是空间电压矢量。

首先我们要看逆变器的电路原理图：

Inverter_Circuit

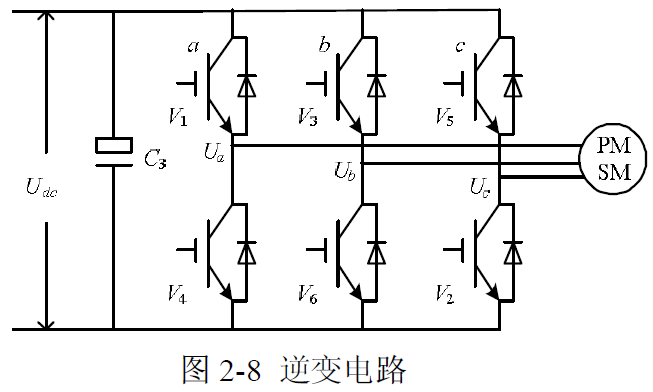
为了便于理解，我们将PMSM的线圈展开绘制出来：

Inverter_Circuit_with_Coil

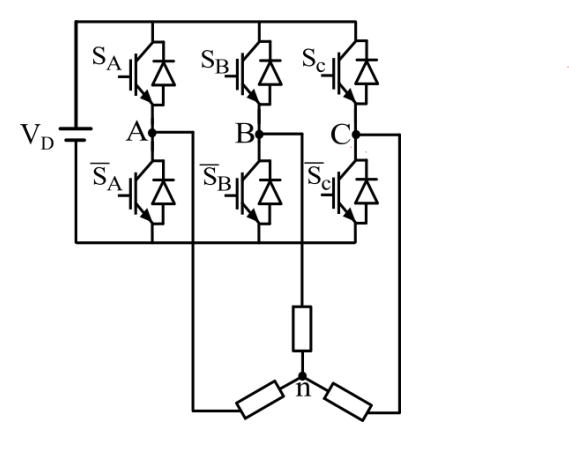
SVPWM算法实际上计算的是上图所示逆变器的六个开关何时导通，何时切断。我们可以看到这六个开关管是两两一组的，也就是形成了三组。对于每一组开关管，与V_D高电位相连的我们称之为上桥臂，而与V_D的低电位相连的我们称之为下桥臂，每一组这个整体我们称之为半桥。

而对于每一个半桥都有两个状态：

• 上桥臂导通，下桥臂截止（定义为状态1）
• 下桥臂导通，上桥臂截止（定义为状态0）

三个半桥就有2³个状态，也就是000、001、010、011、100、101、110、111

• 空间电压矢量：我们将上述的三个桥的状态的组合就定义为空间电压矢量U_n = (S_a, S_b, S_c)。之中有6个非零矢量和2个零矢量（U₀ = (0, 0, 0),  U₇ = (1, 1, 1)）可以看出零矢量状态下电机三相间电压都为0不产生转矩。我们将矢量画在ABC坐标系下（也就是由三相电流组成的坐标系中）

Space_Vector_Diagram

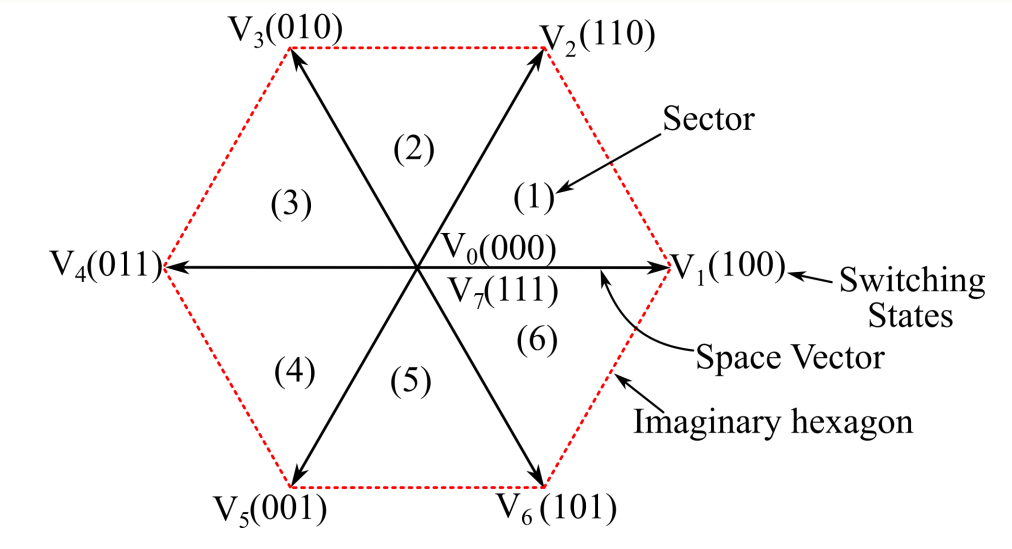
其中，V₁(1, 0, 0)与I_A相同，V₃(0, 1, 0)与I_B方向相同，V₅(0, 0, 1)与I_C方向相同。

它们的端点组成了一个正六边形，同时把平面划分成了六个扇区（也就是图中的（1）、（2）、（3）、（4）、（5）、（6））在每一个扇区，选择相邻两个电压矢量以及零矢量，按照伏秒平衡原则来合成每个扇区内的任意电压矢量。这也正是源自于PWM的核心思想，合理地配置不同基向量在一个周期中的占空比，就可以合成出等效的任意空间电压矢量 ∫₀^TU_refdt = ∫₀^T_xU_xdt + ∫_Tx^{T_x + T_y}U_ydt + ∫_Tx + Ty^TU₀^*dt 写成离散表达式如下： U_ref ⋅ T = U_x ⋅ T_x + U_y ⋅ T_y + U₀^* ⋅ T₀^*

U₀^*指的是两个零矢量，可以是U₀也可以是U₇，零矢量的选择比较灵活，通过合理地配置零矢量可以让空间电压矢量的切换更平顺，可最大限度地减少开关次数，尽可能避免在负载电流较大的时刻的开关动作，最大限度地减少开关损耗。

• 调制方式：

  1. 七段式调制（7-segment SVPWM）

     零矢量对称分布在电压矢量序列的两端，一共7个开关动作，每个周期中相同的矢量对称出现。例如：V₀ → V₄ → V₆ → V₇ → V₆ → V₄ → V₀

     优点：谐波小，对称性好，实现简单也最常用

     Uref所在扇区	开关切换顺序
     （1）区	0-4-6-7-6-4-0
     （2）区	0-2-6-7-6-2-0
     （3）区	0-2-3-7-3-2-0
     （4）区	0-1-3-7-3-1-0
     （5）区	0-1-5-7-5-1-0
     （6）区	0-4-5-7-5-4-0

  2. 五段式调制（5-segment SVPWM）

     零矢量只在一端使用（只用 V0 或 V7），不对称，省略了一端的零矢量插入。例如：V₄ → V₆ → V₇ → V₆ → V₄

     优点：开关频率低

     缺点：谐波较高

  3. 九段式调制（9-segment SVPWM）

     零矢量插入在三处：前、中、后，用更多零矢量来均衡电压和磁链。例如：V₀ → V₄ → V₀ → V₆ → V₇ → V₆ → V₀ → V₄ → V₀

     该方法使用很少，开关频率最高，损耗也最大，控制逻辑也复杂

  更多调制方式可以阅读相关文献，这里不再深入探讨。

Clark变换，Park变换，反Park变换

Clark变换

三相电路计算困难，将三相等效成二相。根据基尔霍夫电流定律（KCL）：任意时刻流入节点的电流和等于流出节点的电流和。因此我们只需要知道其中两个电流就可以推导出第三相的电流。其变换过程和变换矩阵如下： 比例系数K的值为 ，则转换矩阵为：

K为何是？

Clark 变换的矩阵本身并不保持矢量长度（不是正交变换），所以变换前后的矢量模长（幅值）会变化。为了让变换前后的幅值不变，就需要再乘一个比例系数。

若要进行等功率Clark变换则

若想更深入了解可查看这篇文章

经过如上Clark变换，就成功将三相电流变为了新的两相电流，但对于控制两相正弦波电流来说仍然是一件困难的事情。

Park变换

若要将正弦的两个变量转为常量来控制，则需要让坐标系跟着两个变量一起旋转。也就是坐标系和新的两相电流的矢量相对静止了（这么表述肯定不严谨，但是最本质的思想是这个意思）。其变换过程如下： 接下来我们就可以对I_d和I_q来进行控制了，经过如上变换将大大降低我们对电流控制的难度。而这两个量所代表的物理意义为转子旋转的径向和切向这两个方向的变量。其中：I_q为切向电流分量，I_d为径向电流分量，我们也需要尽力把它控制为0，

反Park变换

即为Park变换的逆变换

FOC控制流程

先附上FOC控制流程的PID环

FOC_PID_White

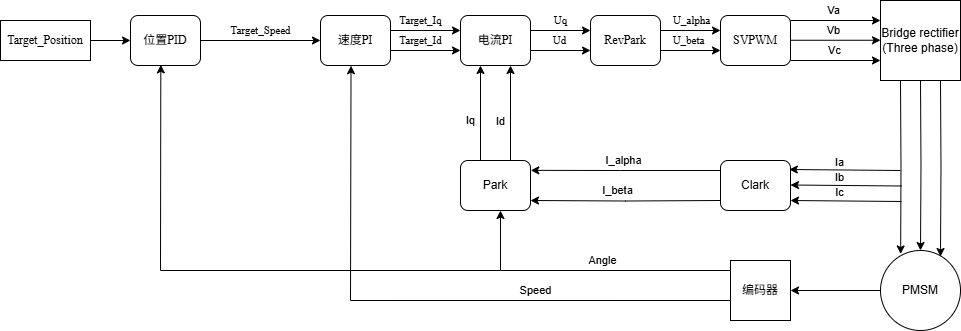
图片中Target开头的代表设定值，即用户希望的值的大小

该PID是常见的位置-速度-电流三环控制，其中位置可以只用P项或者PI项。在位置控制中，由于电机转速很低，所以编码器微分得到的角速度不一定准确，因此往往去掉速度环而直接使用位置-电流双环控制。可以看到，前文的知识点都是在为FOC控制的电流环服务的，由此可见电流环的重要程度非常高。